My Blog
Hypothesis Testing
using computer simulation.Code for Quiz 13.
Bootstrapping
Code for quiz 12.
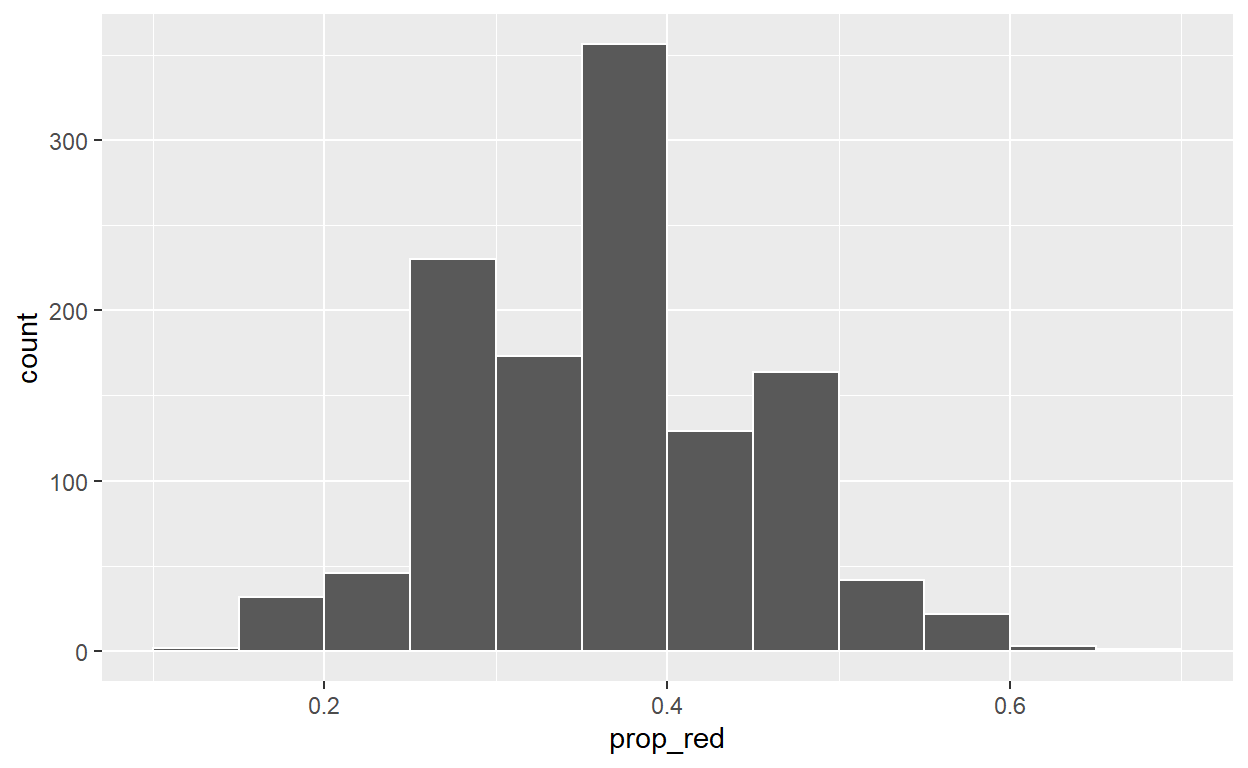
Sampling
Code for Quiz 11.
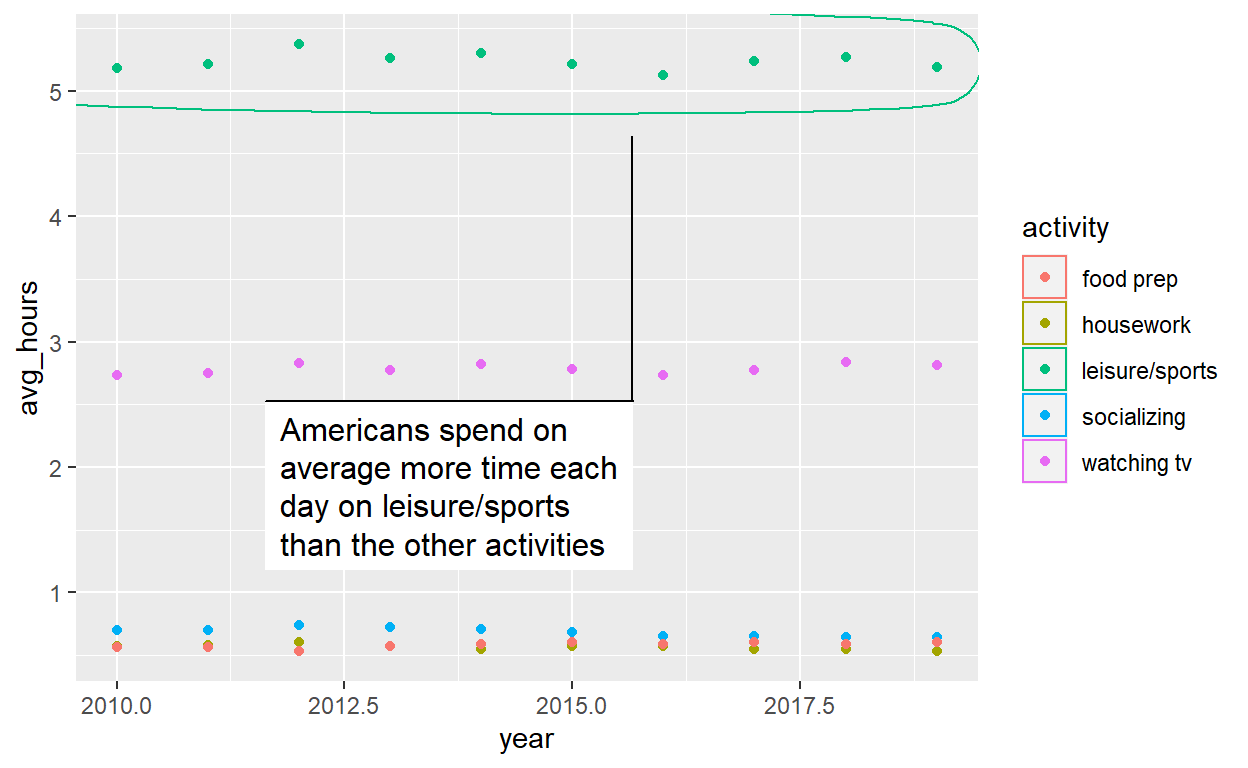
Data Visualization
Code for quiz 9
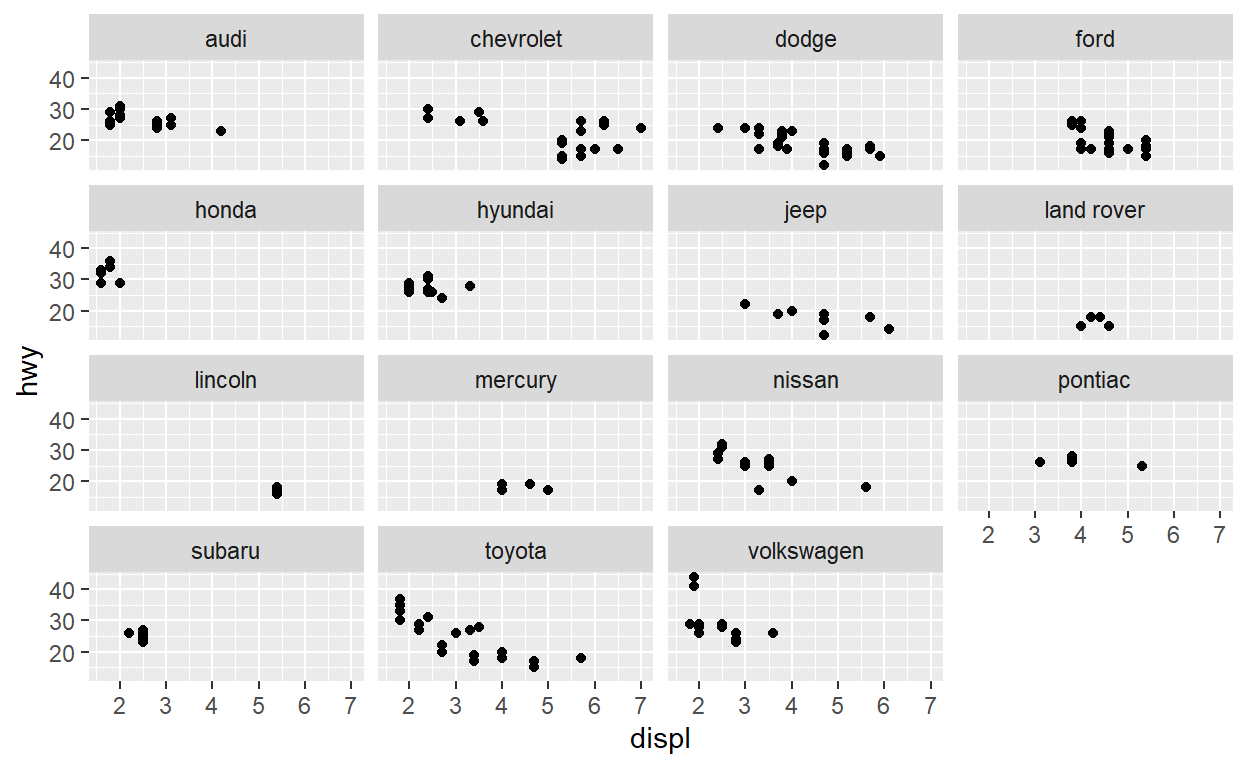
7: Exploratory-analysis-II
Data Visualization, part 2. Code for Quiz 8.
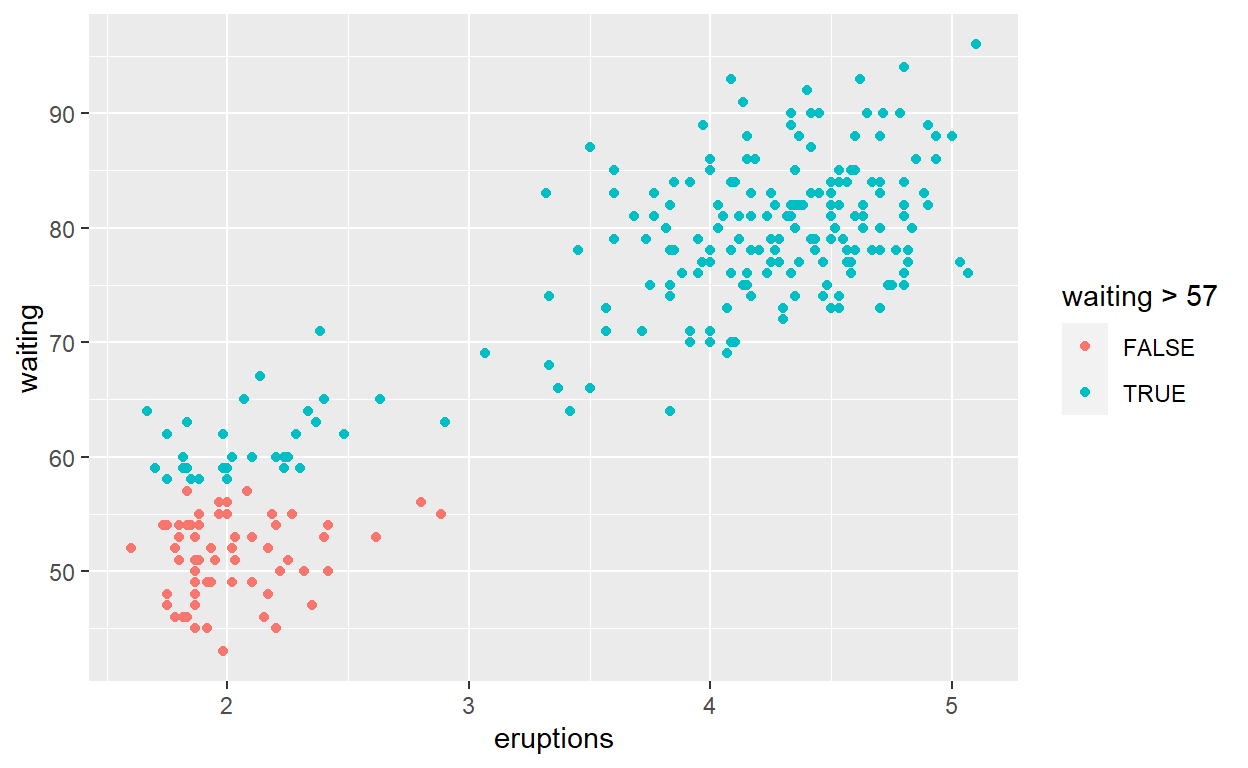
Exploratory analysis
Data visualization, part 1. Code for Quiz 7.
Joining Data
Code for Quiz 6, more dplyr and our first interactive chart using echarts4r.
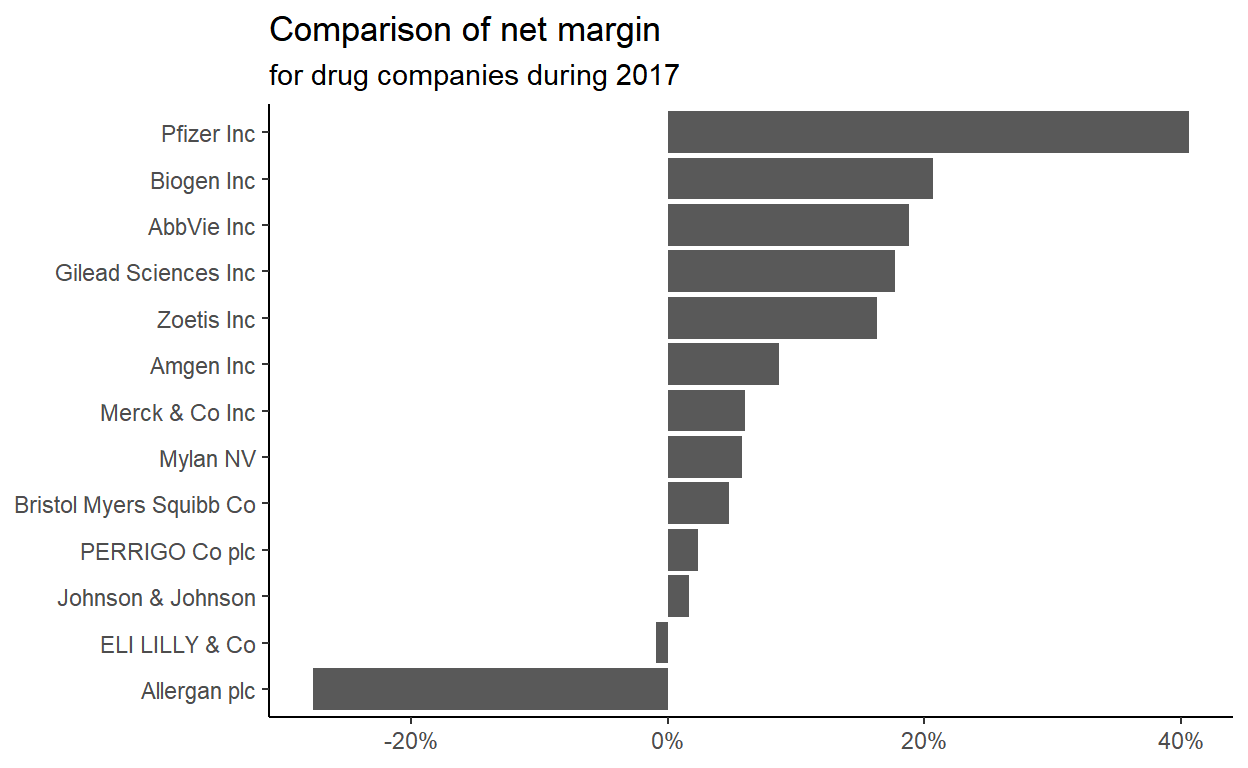
Data Manipulation
Code for quiz 5 More practice with dplyr functions.
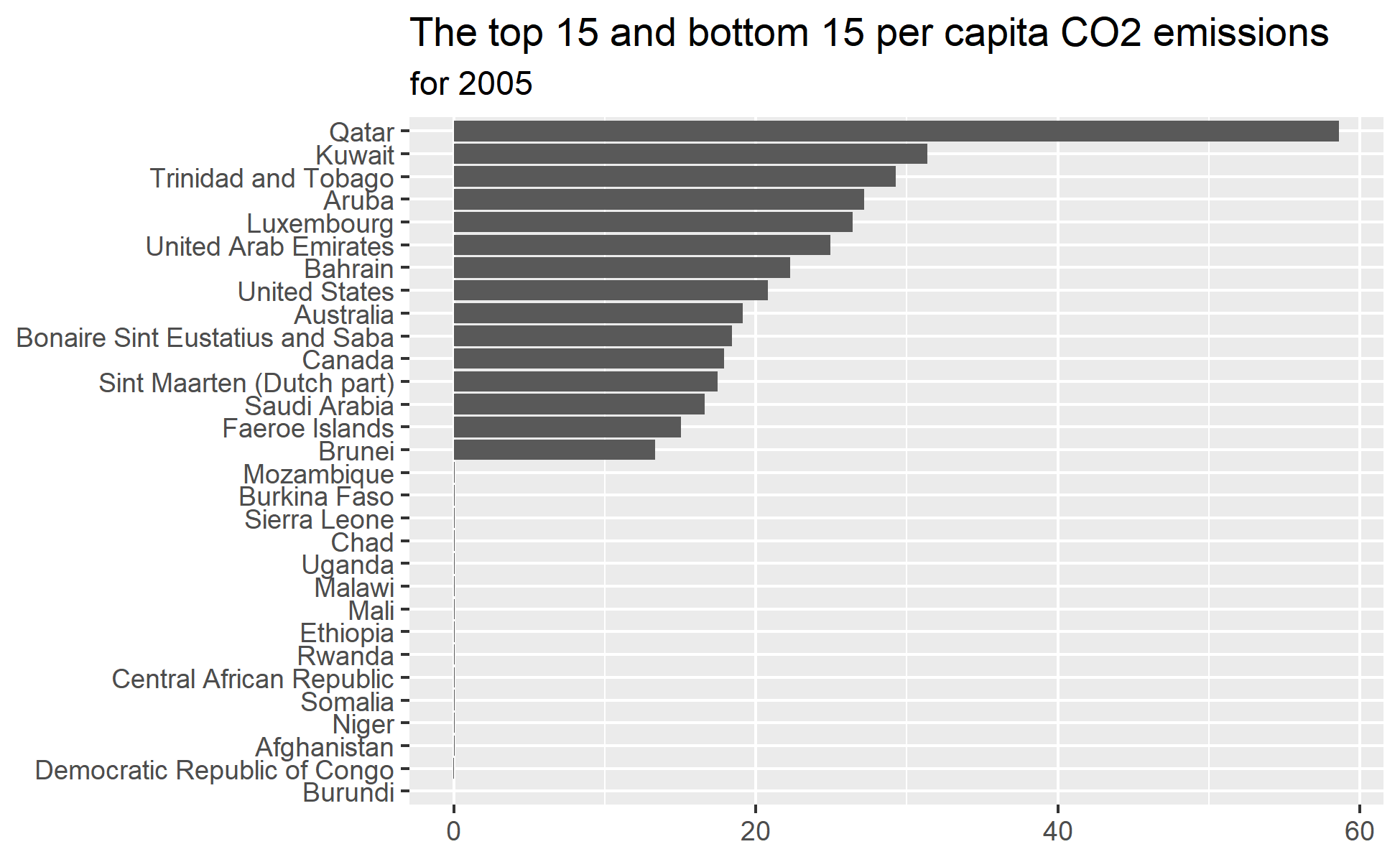
Reading and Writing Data
A short description of the post.
introduction to dplyr
Code and text for Quiz 3
Summary statistics
Comparison of r and excel